از مدل های اتمی تا پیدایش اسپین

به قسمت پنجم، گذری بر فیزیک کوانتوم خوش آمدید. اگر ۴ قسمت قبلی را دنبال کرده باشید، تاکنون اطلاعات جامعی درباره‌ی مکانیک کلاسیک، فیزیک کلاسیک، نارسایی‌‌های فیزیک کلاسیک و نسبیت دارید.

در این قسمت از مجموعه به ادامه‌ی برداشتن گام‌های کوتاه اما عمیق‌مان برای وارد شدن به دنیای فیزیک کوانتوم ادامه می‌دهیم. در این مقاله، روایت پیشرفت‌های فیزیک کوانتومی را شرح می‌دهیم و در بعضی مباحث، گریزی به قسمت سوم نیز خواهیم داشت.

باتوجه به اینکه در قسمت سوم و چهارم این مجموعه، ناچارا مجبور به استفاده‌ی گسترده از روابط ریاضیاتی شدیم، در نظر داشتیم تا در این قسمت کمی از لحاظ تاریخی ماجراهای مربوط به فیزیک کوانتوم را بررسی کنیم و بیشتر به روایت‌گری علم که از نظر اینجانب، یکی از شیرین‌ترین کارهای ممکن است بپردازیم.

اگر به خاطر داشته باشید، اولین بحث نارسایی فیزیک کلاسیک، بررسی تابش جسم سیاه و اتفاقات گسترده‌ی مربوط آن به بود. همان طور که می‌دانید، پس از رخ دادن فاجعه‌ی رایلی-جینز در نهایت این معما، توسط انیشتین و به کمک استفاده از رابطه‌های پلانک رخ داد.

هنگامی که رابطه‌ی پلانک را بیان کردیم، کمیتی به نام h را تعریف کرده و آن را ثابت پلانک نامیدیم. در آن‌جا به‌صورت گذری از h عبور کردیم، اکنون شاید بد نباشد، اندکی درباره‌ی تاریخچه‌ی این h جادویی و ماجراهای مربوط به آن بدانید.

h جادویی

ماکس بورن، فردی از نسل فیزیکدانان نظری بود، که به پیروی از پلانک، در ساختن بنای جدید نظریه‌ی کوانتومی بر شالوده‌های پلانک، یاری می رساند. او به شگردها و مانورهای فریبنده ساده‌ای که پلانک را به فرمول تابش رسانده بود، چنین می نگریست:

رابطه‌ی پلانک، یکی از معتبرترین و پر معنی‌ترین برون یابی‌هایی است، که تاکنون در تاریخ فیزیک به عمل آمده است؛ این رابطه شهود فیزیکی تقریبا مرموزی را آشکار می‌کند.

نه تنها این فرمول، یک فرمول تجربی دقیق، ساده و مفید برای کنترل و همبستگی داده‌ها بود، بلکه در ذهن پلانک چیزی بیش از این بود. این فقط یک فرمول تابش نبود، فرمول تابش معینی، قانون نهایی موثق حاکم بر تابش جسم سیاه بود و به معنی دقیق کلمه این فرمول می توانست، به عنوان اساس یک نظریه به کار گرفته شود و حتی چنان که که مشخص شد، یک نظریه انقلابی باشد!

بدون تردید پلانک سخت در تعقیب و تنظیم آن نظریه بود، او چنین می‌نویسد:

از همان روزی که من (قانون تابش) را فرمول‌بندی کردم، وقت و انرژی من صرف به دست آوردن معنی فیزیکی حقیقی آن شد!

مارتین کلاین، تاریخ نویس علم، می‌نویسد؛ پلانک هنگام نزدیک شدن به این مسئله، بار دیگر از الهه آنتروپی الهام می‌گرفت. اگر یک مفهوم وحدت بخش در دوره‌ی کار علمی طولانی و مفید ماکس پلانک وجود داشته باشد، بدون شک آن مفهوم آنتروپی است.

پلانک سال‌های متمادی را وقف پژوهش و مطالعه آنتروپی و قانون دوم ترمودینامیک کرده بود و یک رابطه‌ی بنیادی آنتروپی-انرژی در به دست آوردن قانون تابش او جنبه حیاتی داشت. اینک هدف بلندپروازانه‌تر از یافتن یک رابطه‌ی آنتروپی-انرژی نظریه‌ای بود، که در مسئله جسم سیاه کاربرد داشته باشد.

لودویک بولتزمن قانون دوم ترمودینامیک را به عنوان یک قانون احتمال تعبیر کرد. او چنین استنتاج کرد، که اگر احتمال یا بی‌نظمی نسبی برای حالت یک سیستم W باشد، در این صورت آنتروپی S سیستم، در آن حالت متناسب با لگاریتم W خواهد بود؛ پلانک با یک حرکت ماهرانه‌ی ریاضی، این رابطه را برای مسئله جسم سیاه با نوشتن آن به‌صورت؛

S=klnW

برای آنتروپی كل مولکول‌های در حال ارتعاش موجود در دیواره‌های کوره‌ی جسم سیاه، که پلانک آن‌ها را مشدّدها (resonators) می‌نامید، به کار گرفت.

در این معادله k یک ثابت عمومی و W معیاری از بی نظمی است. گرچه اعتبار ابداع معادله‌ی آنتروپی غالبا به بولتزمن داده شده و امروزه ثابت بولتزمن نامیده می‌شود؛ اما پلاک نخستین کسی بود که به اهمیت بنیادی معادله و ثابت مذکور پی برد.

پلانک با اکراه و نارضایتی به این معادله رسید. این معادله به شیوه‌ی آماری که به وسیله بولتزمن گسترش یافته بود، عمل می‌کرد. نظريه‌ی بولتزمن این درس را می‌آموخت، که به احتمال زیاد هر فرایند بزرگ مقیاس، می‌تواند معکوس شود و در جهت غیرطبیعی، یعنی در جهت کاهش آنتروپی و مخالف قانون دوم ترمودینامیک پیش رود.

به رغم ناسازگاری با واقعیت‌های نجومی، تکنیک‌های کمّی بولتزمن حتی نشان داد، که چگونه می‌توان احتمال نامساعد باورنکردنی را محاسبه کرد. استنتاجات بولتزمن برای پلانک افسانه‌ای عالی به نظر می‌رسید؛ اما در سال ۱۹۰۰ او از کار پژوهشی‌اش، یعنی یافتن راه قابل قبولی برای محاسبه آنتروپی مشدّدهای جسم سیاه، به‌طور فزاینده‌ای ناامید و حتی بی‌توجه شده بود.

او چند راه نادرست را در پیش گرفته بود، در تفسیر آن‌ها دچار خطاهای اساسی می‌شد و خزانه‌ی نظری او تهی شده بود.

هیچکدام از مسیرهای نظری قبلی که با آن‌ها آشنا بود، راهنمای او نبودند، تا با استنتاجی از قانون تابش تجربی‌اش، سرانجام مطمئن شود به کجا باید برسد. به عنوان آخرین چاره، او با جانبداری از بولتزمن، نوعی احتمال‌گرایی آنتروپی و قانون دوم ترمودینامیک را پذیرفت.

برای پلانک، آن طور که بعدها به یکی از همکارانش نوشت، این امر عملی از روی ناچاری بود. او چنین نوشته بود؛

من طبیعتا مایل و مستعد صلح و آرامشم و هرگونه ماجرای مشکوک را طرد می‌کنم؛ اما در آن زمان بی هیچ نتیجه‌ای به مدت شش سال (از ۱۸۹۴ به بعد) با مسئله‌ی تعادل میان تابش و ماده در کشمکش بودم و می‌دانستم که این مسئله برای فیزیک اهمیت بنیادی دارد. همچنین فرمولی را که توزیع انرژی در طیف بهنجار را بیان می‌کند، می دانستم.(منظور قانون تابش تجربی اوست) تعبیر و توصیف نظریه‌ای را می‌باید، به هر قیمتی شده به دست آورد، اهمیتی ندارد که تا چه حد دور از دسترس است!

پلانک روند شمارشی را برای محاسبه بی‌نظمی W در معادله به کار می‌گرفت، که برگرفته از یکی دیگر از تکنیک‌های نظریه‌ای بولتزمن بود. او دست کم به عنوان یک اندازه‌گیری موقتی، در نظر گرفت که انرژی کل مشدّدها از اجزای غیرقابل تقسیم کوچکی به بزرگی ε ساخته شده‌اند.

در این صورت ارزیابی W به عنوان شماری از تعداد راه‌های یک تعداد معین از اجزای انرژی، که بتواند میان تعداد معینی از مشدّدها توزیع شود، ممکن می‌شد و این کار شامل، محاسبه‌ی ترکیبی ساده‌ای بود که ریاضیدانان مدت‌ها با آن آشنایی داشتند.

معادله‌ی آنتروپی، روند شمارشی بر مبنای ابداع اجزای انرژی و یک معادله‌ی آنتروپی-انرژی استاندارد از ترمودینامیک، دسترسی پلانک به هدفش را تقریبا(نه به شکل کامل)فراهم آورد، هدفی که یک استنتاج نظریه‌ای از قانون تابش او بود. گام دیگری باید برداشته می شد، استدلال او توفیقی حاصل نمی‌کرد، مگر آن که او فرض می‌کرد انرژی ε اجزای مذکور، متناسب با فرکانس ارتعاش مشدّدها است، یعنی

ε = hv

که در آن h ثابت تناسب است. اگر او اندازه‌ی اجزای انرژی را به این طریق بیان می‌کرد، سرانجام می‌توانست قانون تابش خود را استخراج کند و داده‌های جسم سیاه را برای محاسبه‌ی مقادیر عددی دقیق دو ثابت h و k به کار رفته در نظریه‌اش، به کار گیرد.

این مسیر نظریه‌ای پلانک برای قانون تابش او بود، که خلاصه‌ی آن در اواخر سال ۱۹۰۰ به انجمن فیزیک آلمان به اختصار گزارش شد. پلانک دلگرم بود، که سرانجام میوه نظریه‌ای را که برای آن تلاش کرده است، یعنی نظریه عمومی برهمکنش تابش با ماده در دست دارد؛ اما به‌طور دردناکی آگاه بود که برای رسیدن به این میوه، درباره‌ی یک مورد نظریه‌ای نه چندان پیچیده کار دشواری را به عهده گرفته است.

او از محاسبه‌ی آنتروپی آماری بولتزمن استفاده کرده بود. رویکردی که هنوز برای خودش مورد بحث بود. او تکنیک بولتزمن را به طریقی اصلاح کرده بود، که مفسران آن را تردید پذیر می‌دانستند.

 ابراهام پایس، یکی از بهترین وقایع نگاران تاریخ نظریه‌ی کوانتومی، اعتقاد دارد، که سازگاری پلانک با روش بولتزمن نوعی سرکشی است.

کار سرکشانه‌تر پلانک استفاده از اجزای انرژی ε در بسط شناسه‌ی آماری اوست. روال و روند او مستلزم این فرض بود، که انرژی یا حداقل انرژی گرمایی مشدّدهای مادی، یک خاصیت دانه‌دانگی ذاتی و کاهش ناپذیر، مجسم شده در کمیت‌های ε داشته باشند. اما کوچکترین اصلی در ادبیات پذیرفته شده‌ی فیزیک کلاسیک جهانی وجود ندارد، که اعتباری به این ایده دهد. اصول تثبیت شده، که پلانک هم در گذشته، مانند هر کس دیگر از آن صادقانه طرفداری می‌کرد، این بود که همه نوع انرژی به‌صورت یک پیوستار وجود دارد.

هرگاه یک مشدّد یا هر چیز دیگری انرژی‌اش تغییر کند، این تغییر در مقادیر پیوسته صورت می‌گیرد، نه در بسته‌های ناپیوسته آن طور که توصیف پلانک پیشنهاد می‌کند!

فن تخصیص انرژی به‌صورت اجزای کوچک شبه ذره‌ی مورد مطالعه بولتزمن، تنها یک ترفند ریاضی برای یافتن احتمال‌ها بود. در نهایت بولتزمن با فرض اینکه اجزای انرژی بسیار کوچک‌اند، ترتیب بازگشت به پیوستار را داد. طبیعتا، پلانک با استفاده از همان ترفند، امیدوار بود از درگیری و تعارض با اصول پیوستاری کلاسیک، دوری گزیند. اما در کمال شگفتی، نظريه‌ی او این فرض را مجاز نمی‌دانست، که اجزای مذکور به هر مقدار دلخواهی کوچک باشند؛ چرا که ثابت h در معادله‌ی دومی نمی‌تواند صفر باشد.

پلانک امیدوار بود که h بداقبال و در حقیقت ساخت انرژی دالّ بر آن، مصنوعات غیرضروری شناسه‌ی ریاضی‌اش باشد و اینکه کار نظریه‌ای بیشتر با مفروضات کمتر دشواری او را به نتایجی که می‌خواهد، سوق می‌دهد.

او در حدود هشت سال بر این عقیده، که سرانجام دید کلاسیک پیروز خواهد شد اصرار می ورزید. او کوشید تا ثابت h را به نحوی به چارچوب نظریه‌ی کلاسیک متصل کند؛ اما این ثابت در برابر چنین تلاش‌هایی از خود مقاومت نشان می‌داد.

سرانجام پلانک دریافت که عاقبت تلاش او، برای استخراج فیزیک جدید از فیزیک قدیمی، شکست و بی‌ثمری است. اما این شکست برای پلانک آن طور که خودش اعتقاد دارد؛

 تمام و کمال روشن نگری بود. اکنون من به عنوان یک واقعیت می‌دانم، که اجزای انرژی در فیزیک نقشی بسیار مهم‌تر از آنچه در اصل، آمادگی مواجهه شدن با آن را داشتم، دارد و این بازشناسی مرا وادار کرد، تا به وضوح به دنبال ارائه روش‌های کاملا جدید برای تحلیل و استدلال در برخورد با مسائل اتمی باشم!

معنی فیزیکی ثابت h پنهان بود؛ اما برای پلانک زحمت زیادی نداشت تا نتایج مهم فیزیکی را از ثابت همتای آن یعنی k استخراج کند. او با مراجعه به محاسبه‌ی آماری بولتزمن از آنتروپی یک گاز کامل، راهی یافت تا با استفاده از مقدار k، خودش عدد آووگادرو را محاسبه کند. عدد آووگادرو، تعداد مولکول‌ها در یک کمیت استاندارد و یا کمیت مولی از هر ماده‌ی خالص است.

برآورد این محاسبه بسیار بهتر از هر عدد آووگادروی دیگر موجود در آن زمان بود؛ اما این امتیاز تا مدت‌ها شناخته نشده بود. مقدار عدد آووگادروی پلانک به او امکان می‌داد، تا بار الکتریکی الکترون را محاسبه کند و این نتیجه نیز نسبت به اندازه‌گیری‌های معاصرش بهتر بود.

این نتایج برای پلانک اهمیتی برابر با قانون تابش داشت. آن‌ها شواهدی وسیع‌تر از مفهوم نظریه‌اش و فراسوی کاربرد برای تابش جسم سیاه بودند. او در پایان مقاله‌ی سال ۱۹۰۰ خود می نویسد؛ اگر نظریه درست باشد، تمامی این رابطه‌ها نمی باید به‌طور تقريبی، بلکه باید به‌طور مطلق معتبر باشد.

در محاسبه‌ی عدد آووگادرو و بار الکتریکی، پلانک توانست احساس کند، که نظریه‌ی او سرانجام به چیزی مطلق نفوذ کرده است.

تا حدی به علت تلاش‌های خود پلانک که گاهی تردید آمیز بود و تا حدی به علت تلاش‌های نسل علمی جدید کمتر سرکوب شده، نظریه‌ی پلانک، از جمله ناپیوستگی‌های انرژی تثبیت شد. اما راه پذیرش کامل این نظریه، طویل و پر پیچ و خم بود. حتی توسعه‌ی واژگان آن نیز کند بود. اجزای انرژی پلانک سرانجام کوانتوم‌های انرژی نام گرفتند، گرچه واژه لاتین کوانتوم به معنی کمیت، قبلا در زمینه دیگری به کار برده شده بود. توسعه‌ی اساسی نظریه‌ی پلانک، به وسیله‌ی کار دیگران، تا حدود سال ۱۹۱۰ طول کشید و وجه تمایز نام رسمی آن با عنوان نظریه کوانتومی مشخص شد!

بور؛ یک فیزیکدان کامل

در قسمت سوم این مجموعه مقاله، به بررسی مدل‌های اتمی رادرفورد و نیلز بور پرداختیم. اما اکنون شاید بد نباشد، کمی با تاریخ همراه باشیم و سفری کنیم به سال‌های آغازین قرن بیستم، هنگامی که فیزیک کوانتوم، به چشم به جهان گشوده بود و فیزیکدانان مختلف در تلاطم و کشمکش برای یافتن بهترین توجیه برای آن بودند.

نظریه‌ی کوانتومی موفقیتی یک شبه نبود. پذیرش آن طی نخستین دهه‌ی تاریخ تولدش تردید آمیز بود و دست اندرکاران نادری داشت. در سال ۱۹۱۰ اصول موضوع پلانک کم یا بیش مشخص شده بود؛ اما غالبا در مسائل مربوط به تابش و حالت جامد به کار گرفته می شد و تقریبا هرگز در قلمرو اتم‌ها و مولکول‌ها به کار نمی‌رفت.

در تابستان سال ۱۹۱۳ در فیلوزوفیکال مگزین، نخستین سلسله مقالاتی پدیدار گشت که آغازگر تغییر وضع بود. نویسنده این مقالات نیلز بور، فیزیکدان دانمارکی بیست و هشت ساله با شخصیتی بی‌همتا بود. نظریه بور رفتار اتم‌ها، به خصوص اتم‌های هیدروژن را با مخلوط دقیقا مرتبط شده، از اصول موضوع پلانک و مکانیک کلاسیک کپلر و نیوتون توصیف می‌کرد. بور این نظریه را، با موفقیت چشمگیری در مورد نقش‌های زیبای طیف گسیل شده از گاز هیدروژنی که به‌طور الکتریکی برانگیخته شده بود، به کار برد.

(دستگاه فیزیکی آن شبیه چیزی است که در لامپ‌های نئون به کار می‌رود) این امر برای فیزیکدانان آن زمان دستاوردی باور نکردنی بود. متخصصان طیف نمایی، آزمایشگرانی که نظم موجود در طول موج‌های نور (طیف) گسیل شده از اتم‌ها و مولکول‌ها را بررسی می‌کنند، مدت‌ها کارشان را بدون استفاده از یک نظریه انجام می‌دادند، به‌طوری که امید خود به یافتن آن را از دست داده بودند. مقالات بور امید تازه‌ای هم برای طیف نمایی و هم برای نظریه کوانتومی بود.

نقش بور در این مورد تا حدی به خوش اقبالی او باز می‌گشت. نظریه‌ی کوانتومی در سال ۱۹۱۳ به قدر کافی سر برآورده بود، که دیگر نمی‌شد، اهمیت آن در فیزیک اتمی را دیگر نادیده گرفت. با این حال وظیفه‌ی بور کار ساده‌ای نبود، مهارت و احساس شهودی بسیاری لازم بود، تا مخلوط کارآمدی از فیزیک کلاسیک و فیزیک کوانتومی به وجود آید. اینشتین می‌گفت؛ که او نیز ایده‌های مشابهی داشته؛ اما شهامت توسعه و پروراندن آن‌ها را نداشته است. برای اینشتین کاربرد حساس فراهم آوردن بنیاد نامطمئن و متناقض نظریه کوانتومی با مسائل اتمی یک معجزه غیرقابل باور بود.

بور چیزی بیشتر از شاهکارهای نظری انجام داد. او تقریبا به تنهایی، مکتب بزرگی از فیزیک نظری و تجربی در کپنهاگ ایجاد کرد. مؤسسه‌ی بور در ۳ مارس ۱۹۲۱ افتتاح شده و به سرعت شگفت انگیزی فیزیکدان‌های جوان آلمان، انگلستان، روسیه، هلند مجارستان، هند، سوئد و امریکا را جذب کرد. بور مکانی را برای زندگی و کار آنان فراهم کرده بود، چرا که در آن زمان مقامات آکادمیک نادر و فیزیکدانان نظری، مانند هنرمندان، تنگ دست بودند!

افراد حاضر در این مجموعه، تنها مشغول پژوهش‌های علمی نبودند، بلکه بسیاری از اوقات فراغت و تفریح خود را نیز در کنار یک دیگر می‌گذراندند و به‌طور مثال در زمان‌های مختلف تنیس روی میز بازی می‌کردند یا فیلم می‌دیدند؛ اما از داخل همین جو ظاهرا ساده و صمیمی، کارهای بسیار درخشانی پدید آمده است. نام و دستاوردهای آنان حکایت بخش بزرگی از رویدادهایی است، که در دوران بحرانی و سرنوشت ساز سال‌های ۱۹۲۰ و سال‌های ۱۹۳۰ در فیزیک کوانتومی به وقوع پیوست. رابرت اوپنهایمر درباره این دوران و ضرورت نقش بور در آن چنین می‌نویسد:

زمان قهرمانانه‌ای بود. کار، کار یک نفر نبود، بلکه همکاری مشترکی میان تعداد بسیاری از دانشمندان از کشورهای متفاوت را شامل می‌شد، گرچه از ابتدا تا انتها روح فوق العاده خلاق و منتقدانه، نیلز بور این اقدام بزرگ را راهنمایی، کنترل و سرانجام به شکل نهایی تغییر یافته‌ای تبدیل می‌کرد.

بور در عین نفوذ بسیار بالا، ویژگی‌های خاص و منحصر به فرد خود را داشت؛ سخنرانی‌های او احتمالا نه از لحاظ صوتی مناسب بود و نه به‌طور کامل قابل فهم بود، با وجود تلاش بسیار، مقالات و کتاب‌هایش غالبا تکراری و حجیم بود و پرسش‌های بدون شرمندگی او در باره موضوعات پیش پا افتاده ویژگی‌هایی بودند، که از این مرد حکایت‌های خنده داری، ساخته بود. شوخی‌های او محدود به شش جوک بود. با وجود تمام این حرف‌ها، شخصیت او مؤثر و نافذ بود. بور با صراحت لهجه‌ی خوشایند و صمیمانه‌ای سخن می‌گفت، که شاگردان، همکاران و رؤسا را به شکل یکسان تحت تأثیر قرار می‌داد. به‌طوری که لئون روزنفلد، یکی از همکاران بور درباره‌ی سیل بازدیدکنندگان به کپنهاک می گوید؛ آنان که در پی دانشمند بودند، با مردی به معنی حقیقی کلمه کامل رو به رو می‌شدند.

گشاده دستی و سخاوت بور با پاسخ قابل ملاحظه‌ای جبران می‌شد. ظاهرا، بور نمی‌توانست بدون مصاحبت و همراهی انسان‌های دیگر فکر خلاق داشته باشد. او در سراسر زندگی حرفه‌ای خود، از طریق گفت و شنود با بعضی مخاطبان منتقد، ایده‌های علمی به ذهنش راه می‌یافت، شکل می‌گرفت و تکمیل می‌شد. مخاطبان او از آنان که در مؤسسه در دسترس بودند، انتخاب می‌شدند.

او اندیشه‌هایش را با جمع کوچکی از مخاطبان هماهنگ می‌کرد، به‌طوری که هیچ بخشی از فرایند خلاقش نمی‌توانست بدون یک هیئت مشاور انسانی پیشرفت کند. مقاله‌ها و متن سخنرانی‌های او در جلساتی ناآرام و به‌طور غیر عادی تحکم آمیز نوشته می‌شد، که بعضا به‌صورت تک گویی (مونولوگ) بود. یکی از دستیاران بور به نام اُسکار کلاین صحنه‌ای از اصلاح یک متن سخنرانی بور را برای ما مجسم می‌کند:

من با مداد و کاغذ در کنار میزی نشسته بودم، که بور دور آن پرسه می‌زد و به‌طور متناوب مطلبی را به انگلیسی دیکته می‌کرد و به دانمارکی توضیح می‌داد، در حالی که می‌کوشیدم گفته‌های انگلیسی او را روی کاغذ بیاورم. بعضی اوقات وقفه‌های طولانی در گفتار او ایجاد می‌شد، خواه به این علت که درباره‌ی دنباله مطلب تفکر می‌کرد، یا به این علت که درباره چیزی خارج از موضوع فکر می‌کرد، موضوعی که می‌بایست درباره آن به من گفته می‌شد. همچنین، غالبا کار به این دلیل قطع می‌شد، که ایشان به همراه خانواده برای آبتنی و دوچرخه سواری کوتاه مدت به ساحل می‌رفت.

انرژی و پیگیری او برای کامل کردن یک مقاله تقريبا فوق بشری به نظر می‌رسید. هر کلمه، هر جمله، هر مفهوم و هر معادله می‌بایست بارها و بارها بازنگری و تجدید نظر می‌شد، پس از پنج یا شش پیش نویس که احتمالا آخرين آن‌ها نمونه چاپی بود، بور بدون آن که هنوز نظرش قطعی شده باشد، به گوشه‌ای ساکت و آرامی از مؤسسه، به همراه منشی یا نسخه بردار می‌خزید و تلاش و تقلا همچنان ادامه داشت. تا سرانجام به شکل غیرقابل باور، رضایت خاطر پیدا می‌کرد. پاسخ ولفگانگ پائولیفیزیکدان نامی به یکی از دعوتنامه‌های بور چنین بود که؛ اگر آخرین نمونه چاپی برای او ارسال شود، خواهد آمد!

با پافشاری بی‌امان بر صراحت و وضوح و استعداد وسيع برای استقبال انتقاد از دیگران در گفتگوهای بسیار طولانی، بور ترتیبی داده بود، تا به بعضی از مشکل‌ترین مسائل در فیزیک کوانتومی، از جمله آن‌ها که ماهیتی مفهومی و فلسفی داشتند، نفوذ کند. استدلال‌هایش چنان مبهوت کننده، کامل و دقیق بود که بلامنازع و آسیب‌ناپذیر می‌نمود. تعبیر او از نظریه کوانتومی، به ویژه معماهای آن با نقطه نظرهای اینشتین مغایر و غالبا متناقض بود. در آغاز سال ۱۹۲۷ و در یکی از کنفرانس‌های سلوی و در ادامه آن به مدت بیست سال، بور و اینشتین مناظره دوستانه‌ای درباره معنی فیزیک کوانتومی را ادامه دادند. اینشتین هرگز استنتاج بور را مبنی بر اینکه ریز جهان اتم‌ها و مولکول‌ها در نهایت نامعین است، نپذیرفت و بیشترین سعی خود را برای شکست دفاعیات بور انجام داد. بور همیشه یک پاسخ برای انتقادهای اینشتین داشت و استدلال‌هایش پیروز و قانع کننده بود.

بور سعادت یک ازدواج ایده‌آل را داشت. مارگریت نورلاند بور بانویی محجوب و هوشمند بود. بور صاحب شش پسر شد، پس از سال ۱۹۳۲ آنان در خانه‌ی افتخار کارلز برگ ، شهروندان درجه اول دانمارک، زندگی می‌کردند. روزنفلد در باره‌ی نقش حیاتی مارگریت در این زندگی پیچیده چنین می‌گوید:

وظیفه مارگریت، کار آسانی نبود. بور طبیعتی حساس داشت و دائما به مشوق و محرک، همدردی و تفاهم نیاز داشت. وقتی سروکله بچه‌ها پیدا شد، بور به‌طور بسیار جدی وظیفه‌ی بزرگ خانواده را بر عهده گرفت. همسرش خود را بدون تلاش ظاهری با نقش میزبانی سازگار می‌کرد و شامگاه در خانه‌ی بور با گفت و گوی صمیمانه و شعف انگیز جلوه‌ی خاصی داشت.

بور برنده جایزه نوبل شد. او به روزولت و ترومن رؤسای جمهور امریکا و چرچیل نخست وزیر انگلیس توصیه‌هایی کرد و در هر گوشه از جهان فیزیک شهرت یافت. زندگی ، شخصیت و آرمان‌های او افسانه شد. تنها اینشتین و ماری کوری، در میان دانشمندان قرن بیستم، به چنین مقامات رفيع و بلند آوازه‌ای رسیدند.

انقلابی از جنس دانمارک

نظريه‌ی بور تصویری انتزاعی ارائه می‌کند؛ رفتار اتم‌ها را به شیوه‌هایی نشان می‌دهد، که در جهان اشیا عادی شناخت‌پذیر نیست. بور به ما می‌گوید که الکترون‌های اتم در حرکت مداری‌اند؛ اما این الکترون‌های مدارگَرد، انرژی کوانتیده و محدودیت خاصی دارند، آن‌ها با جهش‌های ناپیوسته که نمی‌توان به‌طور کامل با استفاده از  نظریه آن را توصیف کرد، از مداری به مدار دیگر می‌روند.

این سخن دقیقا به چه معنی است؟ بنا به تشخیص خود بور، هر پاسخی یا دست کم هر پاسخ کلامی محدودیت‌هایی دارد. مشکل این است که ما زبان مناسبی برای بیان این مطلب نداریم. بور در گفت و گویی با هایزنبرگ چنین گفت:

هیچ‌گونه توصیف روشنی از ساختار اتم وجود ندارد؛ تمامی چنین توصیف‌هایی لزوما می‌باید مبتنی بر مفاهیم کلاسیک باشد، که در این صورت دیگر به کار نمی‌آیند. ملاحظه می‌کنید که هر کس برای پروراندن چنین نظریه‌ای می‌کوشد، در واقع آب در هاون می‌کوبد!

هنگامی که می‌خواهیم چیزی درباره‌ی ساختار اتم بگوییم، زبانی نداریم که با آن بیان مطلب برای خودمان مفهوم باشد. از بسیاری لحاظ همچون دریانوردی هستیم، که یکه و تنها به سوی جزیره‌ای دور افتاده‌ می‌رود، جایی که اوضاع و شرایط آن اساسا با آنچه دریانورد می‌داند متفاوت است و از همه بدتر، بومی‌های آنجا به زبانی کاملا بیگانه حرف می‌زنند. او صرفا باید منظور خود را تفهیم کند؛ اما وسایلی برای انجام این کار ندارد. در چنین موقعیتی یک نظریه نمی‌تواند چیزی را به معنی حقیقی کلمه علمی، توضیح دهد. همه‌ی آنچه را که نظریه می‌تواند، امید به انجام آن داشته باشد این است که؛ رابطه‌ها را آشکار کند و بقیه‌ی آن را به ما واگذار کند، تا هرچه بهتر می‌توانیم با آن سروکله بزنیم!

زبان فیزیک اتمی، به عقیده بور، چیزی شبیه به زبان شعر است؛ شعر آن قدرها که با خلق صُوَر خیالی و برقراری ارتباط‌ها سروکار دارد، تقریبا به توصیف واقعیت‌ها توجهی ندارد.

اگر اساس نظریه‌ی اتمی بور توصیفی نبود، اگر این نظریه توجیه قابل اعتمادی از آنچه واقعا درون اتم روی می‌دهد نداشت، پس دقیقا چه فایده‌ای داشت؟ چرا به سرعت موفقیت‌آمیز شد؟ نظریه بور، مانند بسیاری وجوه دیگر فیزیک کوانتومی، ریشه در جهان یافته‌های تجربی و آزمایشی داشت. بور می‌گوید:

 مدل‌های به دست آمده از نظریه او استنتاج شده؛ اما اگر ترجیح می‌دهید که فکر کنید این مدل حدسی بوده است، بدانید که این حدس از آزمایش‌ بوده نه از مبانی نظری!

برخلاف اینشتین، که واقعیت فیزیکی را در قلمرو تفکر ریاضی محض جستجو می‌کرد و غالبا به آزمون‌های تجربی نظریه‌هایش بی‌تفاوتی نشان می‌داد، بور مایل بود در جهت عکس عمل کند، یعنی از یافته‌های تجربی بنیادی به یک مجموعه از اصول موضوع معقول و مؤثر برسد.

اینشتین اصل خلاقیتش را در ریاضیات یافت. اصل خلاقیت بور احتمالا تکیه بر نتیجه تجربی بود. یکی از منابع عمده‌ی الهام بور در ایجاد نظريه‌ی اتمی‌اش فرمول بالمر-ریدبرگ برای خطوط طیفی هیدروژن بود.

بور در سال ۱۹۱۳، تنها چند ماه پس از انتشار نخستین مقاله‌اش درباره نظريه‌ی اتمی، در گردهمایی انجمن بریتانیایی برای پیشرفت علم حضور یافت و متوجه شد، که با همدلی و تفاهم درباره نظریه‌اش بحث می‌شود. جیمز جینز بحث مسائل تابش را با اشاره و یادآوری ایده‌های بدیع بور گشود و گفت؛ فکر می‌کنم باید توضیح قانع‌کننده سری‌های طیفی را ادامه دهیم و اصول موضوع غير مرسوم را با این اظهار ارزیابی کنیم، که تنها توجیهی که فعلا برای این فرض‌ها مطرح می‌شود، فرض جدی موفقیت است!

وقتی اینشتین در سال ۱۹۱۳، نظریه بور را شنید شگفت زده شد و گفت؛ بنابراین فرکانس نور ابدا به فرکانس چرخش الكترون بستگی ندارد و این دستاورد عظيم، یکی از بزرگترین اکتشافات است. اما بودند کسانی که اصول موضوع و بحث تطابق را تصنعی و غیرقابل قبول می‌دانستند.

با گسترش گروه شاگردان جوان و مستعد بور، انتقادها به تدریج تخفیف یافت. به مدت ده سال، نظریه بور و شرح جزئیات آن به وسیله نظریه پرداز مونیخی آرنولد زومرفلد توسعه یافت. زومرفلد مسلط در فیزیک اتمی و راهنمای پژوهش در این زمینه بود. نظريه‌ی بور، همان گونه که منظور او بود، یعنی اساس وحدت یافته برای علم تجربی قبلی طیف نمایی شد. این نظریه و دستاوردهای آن در سال ۱۹۱۹ وقتی زومرفلد این سرودنامه را برای زیبایی‌های کاربرد نظریه کوانتومی در طیف نمایی اتمی نوشت، به نقطه اوج خود نزدیک شده بود؛

آنچه را که امروزه ما می توانیم از طیف بشنویم، یک موسیقی اتمی تمام عیار از کُره‌ها، نغمه‌ی یک کاریلون (Carillon) از رابطه‌های اعداد صحیح کامل، یک نظم فزاینده و هماهنگی در کثرت است.

مهر تایید آزمایش فرانک-هرتز

نظریه‌ی بور در ورای کاربردهایش برای طیف نمایی به‌طوری متمایز وظیفه همه‌ی نظریه‌های بزرگ را انجام داد؛ این نظریه حوزه‌های جدیدی از پژوهش تجربی و نظریه‌ای را کشف و آن‌ها را متحد کرد. یکی از مؤثرترین و شگفت انگیزترین تأییدات مفاهیم بور در سال ۱۹۱۴ به وسیلهجیمز فرانک و گوستاو هرتز (برادرزاده هاینریش هرتز) از مؤسسه‌ی شیمی فیزیک کایزر ویلهلم در برلین گزارش شد. آزمایش فرانک-هرتز تجلی جالب و مشخصی از وجود حالت‌های مانا به عنوان خواص ذاتی اتم‌ها به دست می‌داد. فرانک و هرتز روشی برای ایجاد باریکه‌های الکترون یافتند، که حامل مقادیر متغیر؛ اما کنترل شده‌ای از انرژی جنبشی بودند.

در این روش اتم‌های گاز جیوه را در مسیر چنین باریکه‌ای از الکترون قرار دادند، به‌طوری که انرژی از باریکه‌ی الكترون به اتم‌های جیوه منتقل می‌شد. فرانک و هرتز دریافتند، که وقتی انرژی باریکه به مقدار بحرانی معینی می‌رسد، انتقال انرژی از باریکه به اتم‌های جیوه تقریبا کامل می‌شود و جریان باریکه ناگهان افت می‌کند. از دیدگاه نظريه‌ی بور، الکترون‌ها با انرژی بحرانی باریکه، باعث گُذار بین دو حالت مانای جیوه می‌شدند.

طرح آزمایش فرانک-هرتز چنان مستقیم از پیشنهادهای نظریه‌ای بور، درباره‌ی حالت‌های مانا پیروی می‌کند، که وقتی کسی مقاله‌ی فرانک-هرتز را می‌خواند، تصور می‌کند که نویسنده‌اش تحت تأثیر توصیه‌های بور بوده است، چنان که بعضی از نویسندگان کتاب‌های درسی چنین تصوری داشته‌اند. اما راه‌های پیشرفت علمی ناقص است؛ فرانک و هرتز مقاله ۱۹۱۳ بور را ندیده بودند و حتی اگر هم مقاله را، پیش از جمع آوری نتایج کار خودشان دیده بودند، احتمالا باور نمی‌کردند که چه چیزی را می‌خوانند. اظهارات رُک و راست فرانک درباره‌ی نگرش و طرز فکر آن زمان در برلین نشان می‌دهد، که چه نور ضعیفی به اکتشافات بزرگ علمی می‌تابد:

(بخشی از مصاحبه‌ی فرانک در سال ۱۹۶۰)

ممکن است برای شما جالب باشد که وقتی ما آزمایش‌هایمان را انجام می‌دادیم، نوشته‌های علمی را به قدر کافی نخوانده بودیم و شما می‌دانید چطور چنین چیزی اتفاق می‌افتد. از سوی دیگر، ممکن است فکر کنید افراد دیگری در باره‌ی آن چیزهایی به ما گفته باشند. به‌طور مثال، ما سمینار دانشگاهی بزرگی در آن زمان در برلین داشتیم، که در آن در باره‌ی تمامی مقاله‌های مهم بحث می‌شد؛ اما هیچکس درباره‌ی مقاله‌ی بور بحثی نکرد، آیا می‌دانید چرا؟ دلیلش این است که پنجاه سال پیش، با سطح دانشی که در آن زمان داشتیم، اعتقاد بر این بود که هیچکس گسیل خط طیفی را نمی‌فهمد، به‌طوری که اگر کسی مقاله‌ای در باره‌ی آن منتشر می‌کرد، فرض بر این بود که، احتمالا درست نیست. بنابراین ما آن را نمی‌دانستیم!

گرچه همان طور که درمقاله‌ی سوم نیز، این مدل اتمی را به شکلی جامع بررسی کردیم، بعدها مشخص شد که این مدل نیز نارسایی‌های مخصوص خودش را دارد و بنابراین رد شد؛ اما پیدایش این مدل و مطالب مربوط به آن در زمان خودش، یک تحول عظیم در جریان فیزیک کوانتومی را ایجاد کرد.

حال پس از گذر از نیلز بور، اکنون وارد سومین دهه از قرن بیستم شده‌ایم و دانشمندان نسل دوم، فیزیک کوانتومی در حال مطرح شدن و ارائه‌ی نظریات نوین خود هستند، یکی از این افراد ولفگانگ پائولیاست، که زمانی نیز دستیار نیلز بوهر بوده است.

نسل دوم؛ ظهور مردی استثانایی

روایت جدید نظریه‌ی کوانتومی، که امروزه به نام مکانیک کوانتومیمشهور است، تنها طی پنج سال در خلال سال‌های ۱۹۲۵ تا ۱۹۳۰ متولد شد، رشد کرد و به مرحله‌ی بلوغ رسید. آنچه طی آن پنج سال انجام شد، بیشتر از بیست و پنج سال پیش از آن، یا در واقع طی هفتاد و اندی سال بعد از آن بود. پیشرفت‌های پیش از ۱۹۲۵ دائما با تردیدهای مفهومی مسدود می‌شد.

تعارض‌هایی از قبیل دوگانگی موجی ذره‌ای(در قسمت سوم بررسی شده است) یا تناقض میان نظریه اینشتین درباره ذره‌ای بودن نور و نظریه موجی کلاسیک، آشفتگی و محدودیت ایجاد می‌کرد. در سال ۱۹۲۵ این دشواری‌ها، احتمالا از لحاظ خودمانی شدن موضوع، کمتر دست و پاگیر بود. نظریه‌پردازان دیگر درباره‌ی تفاوت مفهومی در قلمرو کوانتومی نگران نبودند و ایجاد یک فیزیک جدید با پذیرفتن غرابت یا بیگانگی در آن را آغاز کردند.

وقتی حصارهای مفهومی کنار گذاشته شد، پیشرفت به‌طور شگفت انگیزی تسریع شد. برای آنان که بصیرت داشتند، مانند آن بود که مه غلیظی رقیق شده باشد. ناگهان مشاهده در بسیاری از جهات با وضوحی ممکن شد، که هیچ کس انتظارش را نداشت!

فیزیکدانان کوانتومی شکل جدید کار خود را در اوایل سال‌های ۱۹۲۰ آغاز کردند. آنان غالبا نسل دوم فیزیکدانان کوانتومی بودند، یعنی پس از آن که پلانک مقاله‌ی معروفش را در سال ۱۹۰۰ در انجمن فیزیک برلین خواند، متولد شده بودند.

یکی از درخشان‌ترین و با نفوذترین عضوهای این گروه مستعد پائولیبود، که نه تنها سهم عمده‌ی خودش را داشت، بلکه مانند بور در شکل‌گیری کار همکارانش، با بحث‌های طولانی و انتقادی، تأثیرگذار بود. طی سال‌های بحرانی ۱۹۲۰ و ۱۹۳۰ بسیاری از فیزیکدانان کوانتومی احساس می‌کردند، کارشان پایان نیافته است، مگر هنگامی که با پائولی و انتقادهای بی‌امان او مواجه شوند، یا در نبود پائولی، این پرسش را مطرح می‌کردند که؛ پائولی چه خواهد گفت؟

یکی از دستیاران پائولی، رودلف پیرلز، درباره نقش پائولی به عنوان یک منتقد می‌گوید:

بحث کردن درباره کاری ناتمام یا ایده‌ای جدید و تأمل انگیز با پائولی تجربه‌ی بزرگی بود، زیرا درک عمیق و صداقت فکری فوق العاده‌ی او موجب می‌شد، که هرگز مطلبی را با سهل انگاری یا استدلال تصنعی سرهم بندی شده رها نکند.

بیشتر تأثیرگذاری پائولی به عنوان یک منتقد حاصل بی‌توجهی افسانه‌ای بود، که به حساسیت‌های مورد علاقه‌ی همکارانش داشت. او زمانی گفته بود؛ بعضی از مردم نقطه‌های حساسی دارند و تنها راه زندگی کردن با آنان این است، که انگشت روی این نقطه‌های حساس بگذاریم تا آن‌ها به آن عادت کنند.

نمونه‌ای از اظهار نظر پائولی در باره یک مقاله کم اهمیت و تقریبا نامنسجم این بود که؛ حتی غلط هم نیست. یا اظهار نظر دیگری درباره یکی از همکارانش، که مقاله‌های او از کیفیت لازم برخوردار نبود، چنین بود؛ اگر آهسته فکر کنید اشکالی ندارد؛ اما اعتراض من وقتی است که سریع‌تر از آنچه فکر می‌کنید، آن را منتشر کنید!

پائولی اهدافی برای اظهار نظرهای گزنده‌اش در تمام سطوح شایستگی، توانایی و مقام یافته بود. پس از یک مباحثه طولانی با نظریه‌پرداز روسی، لانداو که کارش گرچه درخشان بود، ولی بیانش چندان خوب نبود، در پاسخ به اعتراض لانداو که هرچه او گفته بی معنی نبوده گفت؛ آه، نه، خیلی بیشتر از آن است. آنچه شما گفته‌اید آنقدر مغشوش و آشفته بود، که کسی نمی‌تواند بگوید آنچه گفته‌اید بی‌معنی بوده است یا نه!

تحقیر مقامات احتمالا در دوران نوجوانی پائولی، هنگامی آغاز شد که او شاگرد مدرسه‌ای در مونیخ بود و در واکنش به اظهار نظری که اینشتین در یک سمینار رسمی کرده بود. او از عقب سالن سخنرانی مملو از جمعیت گفت؛ می‌دانید، آنچه را که آقای اینشتین گفت، چندان احمقانه نیست!

اصل طرد

پائولی ابتدا به عنوان شاگردی که به سخنرانی‌های زومرفلد گوش می‌داد، به سوی ناکامی‌ها و معماهای نظریه‌ی کوانتومی کشیده شد. اما به زودی با شرح مبسوط و دقیق زومرفلد از نظریه‌ی بور آگاه شد و کاربرد پیچیده‌ای از آن نظریه را برای ساختار مولکول هیدروژن بسط داد. در عین حال، او که منتقد نظریه‌ی بور-زومرفلد بود، به هم شاگردی خود؛ورنر هایزنبرگ اظهار می‌کند، که کل ماجرا رازگرایی اتمی بود. برای پائولی، باحساسیت غیرعادی گوش او برای هماهنگی‌های استدلال صوری(نوعی گام ریاضی کامل) نظریه‌ی کوانتومی آن زمان به هم ریخته و آشفته به نظر می‌رسید.

پائولی به هایزنبرگ شِکوه می‌کند که؛ همه هنوز در مه غلیظ در جست و جوی چیزی هستند و این احتمالا چند سالی طول می‌کشد، که این مه از بین برود، زومرفلد امیدوار است که، آزمایش‌ها ما را در یافتن بعضی قوانین جدید یاری کنند. او به پیوندهای عددی، تقریبا به نوع اسرارآمیزی از اعداد باور دارد.

از زمان نخستین کار بور معلوم شده بود، حالت‌های معینی نشان می‌دهند، که رفتار اتمی دارای انرژی‌های گسسته‌ای است، که می‌توان آن‌ها را از اعداد صحیحی به نام اعداد کوانتومی محاسبه کرد و اینکه وقتی انرژی اتم تغییر می‌کند، این تغییر به‌صورت جهش‌های کوانتومیمیان این حالت‌های مانا انجام می‌شود. تا حدود ده سال پس از مقاله‌های ۱۹۱۳ بور، بیشتر کار در باره‌ی نظريه‌ی اتمی، بر موضوع اعداد کوانتومی متمرکز بود. یکی از پرسش‌هایی که همواره می‌باید، در ایجاد مدل‌های اتمی براساس اعداد کوانتومی پاسخ داده می‌شد، این بود که چند عدد کوانتومی برای هر حالت الکترون لازم است، تا بتواند رفتار فیزیکی و شیمیایی اتم‌ها را توجیه کند. در ابتدا یک عدد کوانتومی مطرح بود (مدل بور)، سپس دو، بعد سه و سرانجام، بنابر نظر پائولی، چهار عدد!

پائولی دریافت که با تخصیص دادن یک آرایه چهارتایی به الکترون‌های یک اتم برای هر حالت موجود، می‌تواند کارهای جالبی انجام دهد. کلید این مدل مجموعه قواعدی بود، که انتخابی از اعداد کوانتومی را در اختيار الكترون می‌گذاشت.

دو قاعده‌ی ارائه شده به وسیله‌ی بور قابل استفاده بود؛ مجموعه‌ی یکسانی از اعداد کوانتومی برای همه الکترون‌ها در همه اتم‌ها موجود است و الکترون‌ها حالت‌های موجود را طوری اشغال می‌کنند، که ابتدا پایین‌ترین حالت انرژی پُر شود. پائولی اصل کلی‌تری را به این دو اصل افزود که بعدها اصل طرد یا اصل پائولی نامیده شد.

این اصل کمک شایان و غیرقابل انکاری به روشن شدن نظریه‌ی اتمی و مولکولی کرد. پائولی با درجه‌ای از سهولت غیرمعمول در فیزیک کوانتومی اظهار داشت، که مجموعه‌ای از چهار عدد کوانتومی حالتی از الکترون اتمی را توصیف می‌کند، که باید برای آن الکترون بی‌همتا و منحصر به فرد باشد؛ هیچ دو الکترونی در یک اتم نمی‌توانند حالتی را اشغال کند، که دقیقا با مجموعه‌ی یکسانی از چهار عدد کوانتومی مشخص شده باشد!

نظريه‌ی بعدی ثابت کرد، که اصل پائولی برای هر سیستمی از الکترون‌ها به کار می رود. هر جا الكترونها گرد هم آیند(در اتم‌ها، مولکول‌ها یا جامدات) جمع شدن آن‌ها می‌باید، بنابر اصل پائولی باشد، یعنی هیچ دو الکترون مجاور هم نمی‌توانند، از لحاظ فیزیکی به قدر کافی به هم شبیه باشند، تا حالت‌هایی را اشغال کنند که دقیقا دارای مجموعه اعداد کوانتومی یکسان باشد. این غالبا بدان معنی است که، الکترون‌ها صرفا از یکدیگر دوری می‌کنند؛ در اتم‌ها آن‌ها در پوسته‌های هم مرکز جمع می‌شوند.

اسپین

اینکه طبق نظر پائولی به چهار و نه سه عدد، نیاز بود تا داستان الكترون کامل شود، برای مدتی معمای نظری بغرنجی بود. در نظریه اولیه آشکار شده بود، که شمار عدد کوانتومی برای یک حالت الکترون بازتاب تعداد ابعادی است، که الکترون در آن‌ها حرکت می‌کند. یک الکترون اتم در حرکت مداری اطراف یک هسته، در سه بُعد حرکت می‌کند و بنابراین مستلزم سه عدد کوانتومی است؛ اما فقط سه عدد برای توصیف آن لازم است. چه معنی فیزیکی می‌توان به عدد کوانتومی چهارم نسبت داد؟ اگر بتوان به مقایسه با فیزیک کلاسیک اطمینان کرد، پاسخی به‌صورت حدسی آشکار وجود دارد. الکترون‌ها، همچون سيارات ممکن است، علاوه بر حرکت مداری، حرکت چرخشی (اسپینی) به دور یک محور درونی نیز داشته باشند.

این ایده به ذهن چند نظریه‌پرداز، از جمله آرتور کامیون، هایزنبرگ، بور وپائولی خطور کرده بود؛ اما مشکلاتی داشت. از یک طرف، چرخش (اسپین) عادی سیارات و توپ‌های بیسبال حرکت چرخشی در سه بُعد است. اگر چرخش (اسپین) الكترون‌ها به همان طریق باشد، به عدد کوانتومی چهارم هیچ نیازی نیست، در این صورت احتمالا چرخش الکترون‌ها، مانند چرخش توپ بیسبال نیست. آیا ممکن است اسپین الکترون به طریقی مرموز، حرکتی خارج از سه بُعد عادی آشنایی باشد، که زیر بنای فیزیک کلاسیک است؟ پائولی، گرچه درباره‌ی مفهوم اسپین مُردد بود؛ اما باور داشت که عدد کوانتومی چهارم او ارتباط به چیزی ندارد، که بتوان آن را از دیدگاه کلاسیک توصیف کرد!

موضوع در اواخر سال ۱۹۲۵ بدین قرار بود، که وان در واردن اظهار داشت، طلسم شکسته شد. آن چه را نظریه‌پردازان گران قدر از انجام آن بیم داشتند، دو دانشجوی هلندی به نام‌های؛ جورج اولنبک و ساموئلگوداسمیت، در دانشگاه لیدن به سرعت و به آسانی انجام دادند. آنان با الهام گرفتن از پائولی به مبانی مفهوم اسپين الكترون پرداختند. اولنبک استدلال اولیه‌ی آنان را توضیح می‌دهد:

گوداسمیت و من با مطالعه‌ی یک مقاله از پائولی به چنین ایده‌ای رسیدیم. در مقاله‌ی پائولی اصل طرد مشهور او فرمول‌بندی و برای نخستین بار چهار عدد کوانتومی به الکترون نسبت داده شده بود. این امر به‌طور نسبتا صوری انجام شده بود و هیچ تصور عینی و مشخصی همراه آن نبود؛ برای ما، این یک راز بود. ما با این قضیه که هر عدد کوانتومی، متناظر با یک درجه آزادی است و از سوی دیگر با ایده‌ی الکترون نقطه‌ای(با ساختاری که مانند سیارات و توپ بیسبال سه بعدی نبود) و آشکارا تنها سه درجه‌ی آزادی داشت، چنان مأنوس بودیم، که نمی توانستیم معنی عدد کوانتومی چهارم را بفهمیم.

این دو دانشجوی جوان بی درنگ امتیازات نسبت دادن عدد کوانتومی چهارم، به نوع خاصی از حرکت اسپینی موجود برای الكترون‌ها، در قلمرویی فراتر از سه بُعد فضایی معمولی را دریافتند. اما آنان به تدریج شاهد اوضاع نامطلوبی می‌شدند.

آنان با مشاورشان، پل ارنفست استاد فیزیک نظری در لیدن، مشورت کردند، همچنین از بنیان‌گذار مکتب لیدن، هندریک لورنتس، که علاقه‌مند به موضوع بود؛ اما ترغیب کننده نبود، یاری گرفتند. (ارنفست جانشین لورنتس بود) آنان پس از آماده کردن خلاصه‌ای از یافته‌هایشان برای ارنفست، بیشتر درباره‌اش فکر کردند و به ارنفست گفتند، که آنان تصمیم به انتشار ندارند؛ اما ارنفست که در زمینه کارهای علمی آگاه‌تر از آنان بود، گفت مقاله را به یک مجله ارسال کرده است.

در حالی که نظریه‌پردازان شاخص‌تر درباره جزئیات خاص مفهوم اسپین نگرانی و تشویش خاطر داشتند، اولنبک و گوداسمیت فرصت مناسبی داشتند. ارنفست به آنان گفت؛ هر دوی شما به اندازه‌ی کافی جوان هستید، که بتوانید مرتکب یک حماقت شوید!

یکی از افراد بسیاری که در رقابت برای نوشتن یک نظريه‌ی موفق اسپین الکترون، مغلوب شد، رالف کرونیگ دستیار پائولی بود. چند ماه پیش از آن که مقاله‌ی اولنبک-گوداسمیت از طریق ارنفست به یک مجله برسد، کرونیگ به نتیجه گیری‌های مشابهی دست یافته و با پائولی در باره‌ی آن‌ها بحث کرده بود. اما کرونیگ خوش شانسی رقبای هلندی‌اش را نداشت. پائولی با انتقاد طاقت فرسا، او را از انتشار نتیجه‌گیری‌هایش منع کرده بود. پیرلز می‌گوید؛ که در سالهای بعد، پائولی میل نداشت، این داستان را به خاطر آورد.

اسپين الكترون مطمئنا یکی از ایده‌های مؤثر و جریان ساز فیزیک و شیمی قرن بیستم است. با این وجود، اولنبک و گوداسمیت برای نظریه‌شان جایزه نوبلی دریافت نکردند. ادعای کرونیگ ممکن است، یکی از دلایل آن باشد. نه تنها الكترون‌ها بلکه همه‌ی ذرات بنیادی (مانند، پروتون‌ها، نوترون‌ها و پوزیترون‌ها) دارای اسپین و اغلب دارای دو حالت اسپین مجازند. نظریه حکم می‌کند، که اعداد کوانتومی مشخص کننده حالت‌های اسپین ۱/۲ + و ۱/۲ – باشد. (اغلب اعداد کوانتومی دارای مقادیر صحیح هستند؛ اما اعداد کوانتومی اسپین، با مقادیر نیم صحیح، استثنایی‌اند) دو حالت اسپین را تقریبا با محور اسپین بالا برای یک حالت و اسپین پاپین برای حالت دیگر در نظر می‌گیرند.

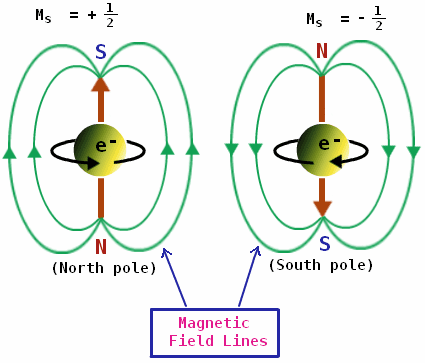
با توجه به اینکه گفته شد اعداد کوانتومی تعداد ابعاد فضایی را نشان می‌دهد، که الکترون در آن حرکت می‌کند، خواننده ممکن است به این فکر بیفتد، که چطور به الكترون اتم هیدروژن که بی شک در سه بُعد حرکت می‌کند، نیز حرکت اسپینی نسبت داده شده است، در حالی که در نظریه‌ی بور به درستی با یک عدد کوانتومی n توصیف می‌شود. الکترون اتم هیدروژن، مانند الکترون اتم‌های دیگر با چهار عدد کوانتومی مشخص می‌شود؛ اما هیدروژن یک مورد خاص است. فقط در هیدروژن و نه اتم‌های دیگر، انرژی حالت‌های الکترون با تقریب خوبی، تنها تابع عدد کوانتومی n است و به سه عدد دیگر بستگی ندارد. بور این خوش شانسی را داشت، که توانست مدل اتم هیدروژن خود را چنان بسازد که انگار دوبعدی باشد!

پایان؛ مردی بالاتر از اینشتین

درک پائولی از مسائل فیزیک در میان معاصرانش عالی بود، به‌طوری که احتمالا حتی اینشتین فراتر از او نبود. بورن یادآور می‌شود؛ از زمانی که او در گوتینگن دستیار من بود، آگاه بودم که او یک نابغه است، نابغه‌ای قابل مقایسه با اینشتین، در واقع از دیدگاه علم محض او شاید حتی بزرگتر از اینشتین بود.

دستاوردهای پائولی، بیان اصل طرد و سهم عمده‌ی او در فیزیک هسته‌ای و فیزیک ذرات، مطمئنا در ردیف استادان فیزیک جدید بود. با وجود این عظمت تمام عیار او برابر با اینشتین، بور و هایزنبرگ نبود!

پائولی تا حدی ذکاوت و درخشندگی خودش را کنترل می‌کرد. گاهی او فیزیک را بسیار خوب می‌فهمید. حسّ منتقدانه او چنان ظریف و گسترده بود، که نمی‌توانست توانایی‌های سازنده‌اش را با تخیل و قابلیت شهودی که بعضی معاصرانش، از آن برخوردار بودند به کار گیرد. پائولی در مورد هایزنبرگ؛ فردی که با انحراف بسیار زیاد از فیزیک کلاسیک و ارائه نظریاتش به شهرت و موفقیت بالایی دست یافت، می‌گوید؛

 شاید یافتن راه برای کسی که با شکوه وحدت فیزیک کلاسیک خیلی آشنا نباشد، بسیار آسان‌تر باشد. شما در آن جا یک فایده‌ی مطمئن و مشخص خواهید داشت.

سپس به‌طور تحسین آمیزی اضافه می‌کند؛ البته کمبود شناخت ضامن موفقیت نیست!

گرچه حس منتقدانه‌ی ظریف پائولی یک قید و بند و بازدارندگی شخصی بود؛ اما برای بسیاری از همکارانش الهام بخش بود. پائولی همچون یک منتقد بزرگ به معنای واقعی کلمه، نظر خود را برای همه کسانی که فراست شنیدن آن را داشتند، بیان می‌کرد؛ گاهی به‌طور دردناکی گزنده؛ اما با صدایی متوازن حاکی از تجربه و بینش.

بسیاری از بهترین کارهای نظری در فیزیک جدید، با حضور پائولی انجام شده است، حضور شخصی که خودش یا روحش، نشسته آنجا، با لبخندی گزنده و تمسخرآمیز گوش می‌دهد!