الگوریتمی برای پیشبینی سلسله اعداد جذاب برای مغز انسان

الگوریتمی ارائه شده است که برپایهی آن میتوانیم دنبالههای اعداد جذاب برای انسان را پیشبینی کنیم.
یکی از ویژگیهای جذاب ریاضی، زیبا بودن آن است. اما اینکه زیبایی در ریاضی به چه معناست، مفهوم پیچیدهای است.
شاید یکی از مشهورترین مثالها برای زیبایی ریاضی، نسبت اویلر (eiπ + 1 = 0) است که ارتباط عمیق بین زمینههای ظاهرا بیربط ریاضی را نشان میدهد. بهعنوان مثال π از هندسه، e و i از جبر، اعداد ابتدایی ۰ و ۱ و عمل جمع و مساوی هم از نظریهی اعداد هستند. چنین مواردی هر کدام مربوط به قلمرویی خاص از ریاضیات هستند و در عین حال با یکدیگر ارتباط دارند و این از عجایب دنیای ریاضی است.
مشخصا وجود چنین ارتباطی نشان از جالب بودن ریاضی دارد. الگوهای ریاضی همیشه جزو آن دسته از مواردی هستند که تنها انسان قادر به تشخیص آنها بوده است.
اما در سالهای اخیر، ماشینها هم ابزاری داشتند که بتوانند با استفاده از آنها، الگوهای خاص را شناسایی کنند. درواقع ماشینها در شناسایی چهره، اشیا و بسیاری از نقشهای بازی، بسیار بهتر از انسانها عمل میکنند. چنین مسئلهای احتمال جالبی را به وجود میآورد: آیا الگوریتمهای یادگیری ماشینی میتوانند الگوهای جالب و ظریف موجود در ریاضی را نیز شناسایی کنند؟ آیا آنها میتوانند در کشف زیباییهای ریاضی نقش محوری بازی کنند؟
خوشبختانه امروزه بهلطف کار پژوهشی چایوا وو در مرکز تحقیق واتسون شرکت IBM در نیویورک، پاسخی برای این گونه سوالها بهدست آمده است. وو یک الگوریتم یادگیری ماشینی ساخته است که میتواند انواع مشخصی از ساختارهای ظریف در ریاضی را شناسایی کند و از آنها برای بیرون کشیدن توالیهای جالب در محیطهای کاملا تصادفی استفاده کند.
تکنیک این الگوریتم با استفاده از یک پایگاه دادهی غیرمتعارف بهنام دانشنامهی آنلاین دنبالههای صحیح یا Online Encyclopedia of Integer Sequences کار میکند که ابتدا در دههی ۱۹۶۰ توسط ریاضیدانی بهنام نیل اسلون ساخته شد و در سال ۱۹۹۶ وارد دنیای وبشد.
توالی و دنبالهی اعداد، به مجموعهای از اعداد گفته میشود که طبق قانون خاص خود در کنار هم قرار گرفتهاند. بهعنوان مثال میتوان به توالی اعداد اول اشاره کرد که تنها بر ۱ و خودشان بخشپذیرند. توالی دیگر، دنباله فیبوناچی است که هر عدد، حاصل مجموع دو عدد قبلی است. دنبالههای دیگری هم هستند که میتوانند قانون خاص خود را داشته باشند مثلا اعداد فردی که از ۷ شروع شوند.
درواقع ریاضیدانانی که دانشنامهی آنلاین دنبالههای صحیح را مدیریت میکنند، اینترنت را به محیطی گسترده برای یافتن توالیهای جالب ریاضی تبدیل کردهاند که نمونههای زیادی از این دست، در آن وجود دارد. این پایگاه داده، توالی ۶۶۶ را هم در خود دارد.
پایگاه داده حتی شامل توالیهایی از اعداد صحیح حاوی عدد ۶۶۷ هستند. دلیل خاص بودن این عدد به زمانی برمیگردد که مردم از فکس استفاده میکردند. شماره تلفن هر مشترک بهعلاوهی ۱، شمارهی فکس آنها بود. بهعبارت دیگر، اگر شماره تلفن مشترکی ۱۲۳۴۵۶۷ بود، شماره فکس آنها ۱۲۳۴۵۶۸ در نظر گرفته میشد. با چنین تفکری، عدد ۶۶۷ به توالی ۶۶۶ بسیار نزدیک بود.
امروزه پایگاه دادهی Integer Sequence حاوی ۳۰۰ هزار توالی است و روزبهروز به این تعداد اضافه میشود؛ چه از جانب افراد حرفهای و چه از طرف آماتورها. بسیاری از آنها با این کار به مسائل جالبی در ریاضی اشاره میکنند.
وظیفهی وو این بود که راهی برای تمییز چنین توالیهایی از انواع تصادفی آن پیدا کند. ایدهی وو این بود که بتواند قوانینی تجربی به دست آورد؛ قوانینی که میزان جالب بودن توالیها از منظر انسانها را پیدا کند. وو گفت:
قوانین تجربی به خودی خود جزو نظریههای ریاضی محسوب نمیشوند؛ آنها درواقع مشاهدات تجربی ناشی از روابطی هستند که در بسیاری از مجموعهی دادههای طبیعی وساختهشده بهدست انسان کاربرد دارند.
نمونهها شامل قانون مور در مهندسی برق، و قانون ۲۰-۸۰ پارتو در اقتصاد است. اینکه چرا چنین قوانینی وجود دارند مشخص نیست؛ ولی بهطور مشخص میدانیم که آنها وجود دارند.
یکی از اصول تجربی که در بسیاری از مجموعه دادهها کاربرد دارد قانون بنفورد است. این قانون توسط ریاضیدانی کانادایی بهنام سیمون نیوکامدر سال ۱۸۸۱ کشف شد. طبق گفتهی نیوکام، لوگاریتمهایی که با رقم ۱ شروع میشوند رایجترند.
طبق چنین قانونی، در یک مجموعهی داده، اعداد بیشتر با ۱ شروع میشوند تا اعداد دیگر. همین ایده در دههی ۱۹۳۰ بار دیگر توسط فرانک بنفورد مطرح و کشف شد.
قانون بنفورد در مجموعه دادههای زیادی کاربرد دارد، از قبوض برق گرفته تا آدرس خیابانها، قیمت سهام و غیره. بنابراین میتوان از این قانون در شناسایی تقلب و کلاهبرداری در حسابهای مالی هم استفاده کرد. البته این قانون در توالیهای تصادفی کاربرد ندارد و برای همین بهراحتی قابل درک نیست.
درواقع اینکه چرا قانون بنفورد در برخی از توالیها کاربرد دارد، مانند پازلی است که تنها خود ریاضیدانان جواب آن را میدانند. اما پرسش این است که این قانون تا چه اندازه در توالیهای مختلف کاربرد دارد؟
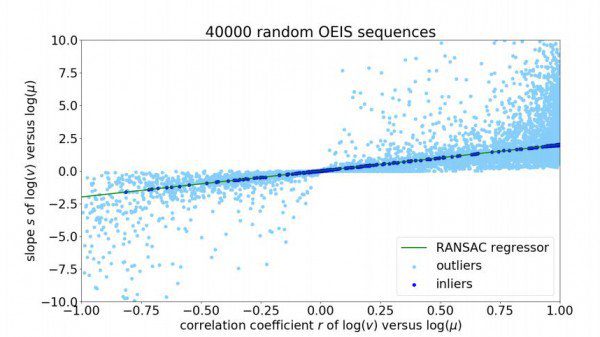
برای درک چنین مسئلهای ما میزان دقت پیشبینی قانون از توزیع ارقام اول در ۴۰ هزار توالی تصادفی از پایگاه داده دانشنامه آنلاین دنبالههای صحیح (OEIS) را اندازه گرفتیم.
مشخص شد که قانون بنفورد بیش از حد انتظار اتفاق میافتد. وو در این مورد گفت:
طبق نتایج، بسیاری (ولی نه همه) از توالیها طبق قانون بنفورد عمل میکنند.
بسط قانون تیلور هم توسط وو کشف شد. سوال بعدی این بود که آیا میتوان از قوانین بنفورد و تیلور برای تمییز توالیهای تصادفی OEIS استفاده کرد؟
دانشمندان برای فهمیدن این موضوع، ۴۰ هزار عدد تصادفی ایجاد شد و آنها را به ۴۰ هزار توالی انتخابشده از OEIS اضافه کردند. وو الگوریتم یادگیری ماشینی را آموزش داد تا توالیهای OEIS را با استفاده از قوانین بنفورد و تیلور شناسایی کند و آنها را از توالیهای تصادفی جدا کند.
نتایج کار حیرتانگیز بود. الگوریتم کارش را با درستی ۰/۹۹۹ و دقت ۰/۹۹۸۴ انجام داد. چنین کاری اهمیت بسیاری داشت؛ چراکه باعث میشد امکان استفاده از روند خودکار برای شناسایی توالیهای جالب فراهم شود.

ریاضیدانانی که وظیفهی مدیریت پایگاه داده OEIS را برعهده داشتند؛ باید هر سال حدود ۱۰ هزار مورد ارسالی را بررسی و پردازش میکردند. کار آنها با استفاده از این الگوریتم خودکار، بسیار راحت میشد.
البته این شیوه محدودیتهای خاص خودش را نیز داشت. ریاضیدانان توالیهای مهم و جالب زیادی را تعریف کردهاند که بینهایت عدد دارند و محاسبهی آنها بسیار دشوار است. اما پایگاه داده تنها بخشی از آنها در اختیار دارد. این تعداد محدود برای تحلیل ماشینی مناسب نیست.
سوال مهمتر اینکه آیا چنین شیوهای میتواند ظرافت و زیباییهای ریاضی را شناسایی کند؟ خود وو هم این سوال مطرح میکند:
آیا یادگیری ماشینی میتواند مشخصههای کیفی دانش علمی را کشف کند؛ بهعبارت دیگر آیا ما میتوانیم بگوییم که نتایج علمی بهدستآمده ظریفاند، سادهاند یا جالب؟
رسیدنبه چنین هدفی کاملا نشدنی نیست. اگر قوانین تجربی مثل قوانین بنفورد و تیلور، شاخصی برای یافتن جالب بودن ریاضیات هستند، پس شاید این الگوریتم بتواند بهعنوان یک تشخیصدهندهی ظرافت (حداقل تا سطحی خاص) عمل کند.
مسلما اگر اویلر (که خود یکی از برجستهترین ریاضیدانان تاریخ است) هماکنون زنده بود، از وجود چنین الگوریتمی شگفتزده میشد.

